相信各位曾經聽過 Grover's search algorithm (如果沒有別緊張，在 QCQI 第 6 章及 QCnote 第 7 章都有精彩的介紹)，這是一個相對於古典搜尋演算法具有二次加速 (quadratic speedup) 的量子演算法。接下來幾天要和大家聊聊的振幅放大 (Amplitude Amplification；以下以 AA 稱之)，其原理正是 Grover's algorithm 的推廣 (有興趣的讀者可以直接看 QCnote 7.3 章)。今天將先介紹基本的 AA 原理，接下來兩天再說說 AA 可以如何變化！

假設我們有一作用於 個 qubit 的量子電路 (不包含測量) 作用於初始態 ，使得

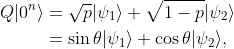
而且 。在這問題中， 是我們感興趣的量子態，因此想放大他的振幅 。和 Grover's algorithm 一樣，我們只關注由 和 所張出的平面。然後我們定義， 為對 的鏡射、 為對 的鏡射；於是， 正是對 的鏡射。有了這些鏡射操作之後，再定義 AA 的演算法如下：

1. 準備量子態 。

2. 重複以下 次 (旋轉 次；鏡射 鏡射 旋轉)：

   1. 對 鏡射 (將量子態乘上 )
   2. 對 鏡射 (將量子態乘上 )

經過上述步驟，我們的量子態變成了

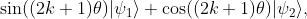
且

大功告成！

但是，如果初始態不再是 ，卻是某一僅有一份的量子態 而且我們沒有如何產生 的資訊 (設 ，而我們不知道 )；此時， 該如何實現？AA 是否就成為不可能的任務？另外，如同 Grover's algorithm，如果旋轉次數 沒有控制得宜，我們感興趣的振幅可能反而變小！這個稱為舒芙蕾問題 (soufflé problem) 的難題又該如何解決？